“Hedging a bet” refers to a betting strategy used to reduce risk or guarantee a profit regardless of the outcome of an event. Essentially, it involves placing a second bet against the original bet that you made, thereby ensuring that you will either minimize your loss or lock in a profit.
Here’s how it works:
Suppose you bet on Team A to win a game, but as the game progresses, you begin to doubt whether Team A will win. In this case, you could place a second bet on Team B. This is known as hedging your bet.
Hedging is essentially a form of insurance — while it might reduce the size of your potential win, it also minimizes the risk of walking away with nothing. So how do you decide if you should hedge your bet? Let’s breakdown how to make that decision.
The Decision-Making Process of Hedging Bets
Back in May 2022, I had a large ticket on a futures bet for Mito Pereira to win the PGA Championship. In fact, I had several large sports betting tickets, totaling $300k if they would have won. On Saturday night, I had the chance to at least partially hedge these outright bets to guarantee a profit. I never seriously considered doing so, for two main reasons: the size of my bankroll, and the expected value of the hedge bet. If I bet against Mito Pereira at that point, I’d be making a negative expected value bet.
However, that’s only a part of the calculus (yes, it’s literally calculus) of a hedging decision. While we normally think about the goal of betting as maximizing expected value, or expected profit, that’s actually not what we should aim to maximize. Deciding if you should hedge a bet depends on three factors:
- How much you stand to win relative to your bankroll
- The true probability of the bet winning
- How much of a premium you are paying in expected value to hedge.
Hedge Betting Strategy – Maximize Bankroll Growth, Not Expected Value
Suppose the Buffalo Bills made it to the Super Bowl and I offered you a bet on the Bills to win the Super Bowl at a +500 price. Would you take that bet? Of course. But how much would you bet? Given that the Bills would have about a 50% chance of winning the Super Bowl in this scenario, the bet has a positive expected value of about 200% (.5*5+.5*-1).
If your strategy is solely trying to maximize your expected value without thinking about bankroll management, you’d mortgage your house, withdraw all your savings, and back up the truck on this bet. If I kept offering you bets like this each week, you’d keep doing the same thing. While you’d maximize your expected value betting like this, you’d go broke rather quickly. All it takes is the bet losing once.
So if it isn’t Expected Value that we should be maximizing, what should our focus should be? Expected Bankroll Growth. I won’t go into all the nerdy details on this, but this is what the Kelly Criterion is all about – maximizing geometric mean instead of arithmetic mean. The way to maximize bankroll growth is to maximize the Expected Value of the logarithm of wealth. When people talk about overbetting your bankroll, they’re referring to betting a percentage of your bankroll that will not optimize your bankroll growth.
Be Aware of Your Sports Betting Bankroll Size
Bankroll size is a critical component of determining whether to hedge a bet or not, and how much to hedge. We launched our Hedge Betting Calculator to help make hedging decisions in a way that is mathematically correct. We take the following inputs:
- Bankroll size
- Probability of your original wager winning
- How much you stand to win
- Odds available for your hedge
From this the calculator determines the optimal hedge amount for bankroll growth.
If I had bet my last $500 on Mito Pereira at 300/1, it would have been a criminally irresponsible bet, and I would never ever ever ever let it ride. Based on my pre-round 4 pricing, the Unabated calculator says I’d optimally want to risk $87,679.38 on Pereira if the best price I could get was -175. Though if I had no money to my name, this would be difficult, especially since Circa does not have a cash out option. This hypothetical situation would be the one situation in the history of the “cash out” feature where it would benefit the bettor.
Let’s say I could get a price of -150 instead of -175. The Unabated calculator says I would optimally risk $87,731.25 on the hedge. The hedge amount is practically unchanged, despite the available bet having a -2.5% expected value as opposed to the -8.1% EV bet at -175. This is because when you overbet your bankroll, you’ve backed yourself into a corner, and are very price insensitive. You hedge because you have to, and will have to pay the price, whatever it is.
Experimenting With The Hedge Betting Calculator
It’s quite fun to use the calculator to plug in some scenarios and see how the optimal hedge amount changes as a function of the hedge bet’s expected value and your bankroll. If we use the initial example, pictured above, and change the current bankroll to $5,000, the optimal hedge decreases to $87,043.75. Not much at all.
Going up by another factor of 10, at a $50,000 bankroll, it’s still correct to hedge a bet of $80,687.5, despite the hedge having a -8.1% expected return. (You should not be betting 1% of your bankroll on 300/1 shots!).
Let’s go up another factor of 10. With a $500,000 bankroll, you should only hedge $17,125 at -175. If I could hedge at -141 (a break-even bet), I’d hedge my full position, just like in the first examples ($87,675 to win $62,181). If you can hedge a sports bet at no loss of expected value, you should always hedge entirely out of your position if you can. You keep the same expected return and minimize variance, which maximizes expected bankroll growth.
When it comes to hedging decisions, you often hear people say it’s a matter of personal preference. It shouldn’t be. If you’re trying to build wealth by betting, there IS a right answer (conditional on having an unbiased estimate of the probability that your initial bet wins).
Rufus’s Magic Number
Let’s go back to my hedging decision. While my probability of Mito winning was 41.5%, I had more exposure than just the one Circa ticket; we’ll round my “stand to win” amount to $300,000. Let’s say I could have gotten access to Betfair and hedged at a price of -170. Given that I saw +160 as the standard price to bet on Pereira there, -170 seems very generous – especially when you account for the exchange costs, money paid to betting partners to get down there, etc. But let’s suspend our disbelief for a moment.
Using a bit of trial and error, I determined that the magic bankroll number is $1,456,431. At a bankroll greater than that, I would have no desire to hedge at that price. And even at a bankroll of just $1mm, I’d only want to hedge roughly one sixth of my exposure.
Hedging decisions are a function of:
(a) how much you stand to win relative to your bankroll,
(b) the true probability of the bet winning, and
(c) how much of a premium you are paying in expected value to hedge.
Exploring Some Other Hedge Betting Scenarios
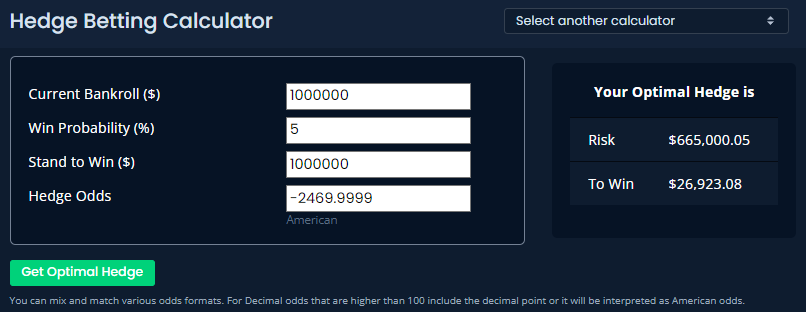
As I mentioned, if a hedge is neutral or positive EV, you should always fully hedge out if you can. In the example below, the hedge is exactly breakeven, and the optimal hedge amount results in a $15,000 profit regardless of who wins (Note that if the hedge is positive EV, your optimal bet amount will result in having a larger position on the hedge winning).
The greater the premium for hedging (the worse the EV of the hedge is), the less it makes sense to hedge the bet. But even more important than the expected value of the hedge is how much you stand to win, in relation to the size of your bankroll. In the example above, the hedge odds where you’d no longer want to hedge anything is -2470 (see below).
But if we leave everything the same and increase the “stand to win” amount from 30% to 50% of bankroll, we see a dramatic shift in optimal hedge amount.
Psychological Considerations of Hedge Betting
Hedge betting is very difficult for some people, because of regret. If you don’t hedge a potential big payday, and the bet ends up losing, you kick yourself for not hedging. If you hedge and the original bet won, you kick yourself for hedging.
Have a process for making these decisions. I have no regret for not hedging my Mito Pereira outrights, because I knew hedging was not the optimal decision. Were my bankroll smaller, I 100% would have tried to hedge (and definitely not regretted it), because it would have been the optimal decision. “Professionals don’t hedge so I shouldn’t” is a huge load of bull. Every situation is different. You can’t paint this decision in broad strokes.
It’s about having a process that you stick to. Whether to hedge isn’t a decision you have to make – the decision has already been made for you. You know what the optimal decision is. You just need to not f*** it up. Whether or not it works out in one instance is immaterial. Your process was good, and in the long run you are putting yourself in the best position to succeed.
